CDMA Technology

The CDMA technology enables access to a shared medium without interference with the use of codes that separate different users within a code space.

CDMA Technology

The main problem is, finding good codes and separating the signal from the noise generated by other signals of the environment.

In order for code to be called the good code, it should exhibit auto correlation property and should be orthogonal to other codes.

Assume a system of vectors starting at the horizon (0, 0, 0). Two vectors are called orthogonal and only if their inner product is zero (0).

For e.g. V₂ = (2, 5, 0) and V₄ = (0, 0, 17)

A code is said to be auto correlated where the inner product with itself is large i.e. not nearer to zero (0).

E.g. barker code is said to be auto correlated and is given by

Barker code : (+1, -1, +1, +1, -1, +1, +1, +1, -1, -1, -1)

Barker code : (+1, -1, +1, +1, -1, +1, +1,+1, -1, -1, -1)

Inner product : (+1, +1, +1, +1, +1, +1, +1, +1, +1, +1, +1) =11 which is not nearer to zero.

Therefore Barter code is auto correlated.

After performing shift operation on the barker code successively the correlation value drops so an absolute value of 1. It stays at this value until it matches again perfectly. So we can use this principle at the receiver to re-construct the original signal after removing the noise.

CDMA Example

Let us consider the following example to explain the basic function of CDMA.

1. Two senders A and B want to send data. Assume CDMA assigns the following keys for A and B.

Ak = 010011 and Bk = 110101. Let sender A wants to send the data bit 1. A_D= 1 and sender B wants to send the data bit 0. B_D = 0.

Let us consider a binary 0 as -1 and binary 1 as +1.

2. Both senders perform spreading during which it multiplies the data bit with the chipping sequence (key).

3. Sender A then sends the signals A_S = A_D x A_K.

A_S = 1 x (-1, +1, -1, -1, +1, +1)

= (-1, +1, -1, -1, +1, +1)

Sender B does the same with its data to spread the signal B_S = B_D X B_K

B_S = -1 x (+1, +1, -1, +1, -1, +1)

B_S = (-1, -1, +1, -1, +1, -1)

4. Both signals (A_S and B_S) are then transmitted at the same time using the same frequency. Therefore these signals are super imposed in space. Assuming that the signals have the same strength, the following signal C is received at the receiver.

5. The receiver now wants to receive data from sender A. Therefore it should find the inner product of C and A_K as shown below.

A_K = (-1, +1, -1, -1, +1, +1)

C = A_S + B_S = (-2, 0, 0, -2, +2, 0)

Inner product = (+2, 0, 0, +2, +2, 0) = 6

Which is much larger than 0 and hence the data at A should be 1.

6. The receiver can now extract data at B by dispreading on B (B_D). Performing dispreading is shown.

C = A_S + B_S = (-2, 0, 0, -2, +2, 0)

B_K = (+1, +1, -1, +1, -1, +1)

Inner product C x B_K = (-2, 0, 0, -2, -2, 0) = -6

Which is much lesser than 0 and hence data much be 0.

This guess can be made only by assuming that there is no noise and also the strength of sender A and sender B is same.

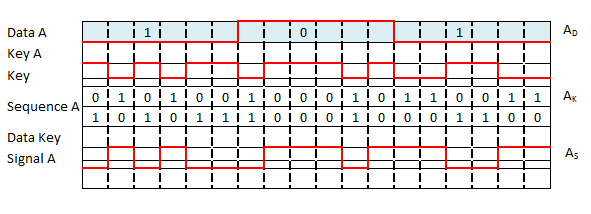
Consider an example, where sender A wants to transmit the bits 101. Let key of A (A_k) be represented as a signal as well as binary sequence. A binary 0 when represented as a signal is considered as a positive signal and a binary 1 as a negative signal.

For spreading here let us use X-OR operation instead of simple multiplication on A_D and A_K resulting in A_S.

Consider the following diagram.

CDMA Architecture