Mean, Median, Mode and Range

Everyday, the word 'average' is applied in different situations like average salary, average height and so forth, but it has the same meaning, commonly the 'center of a distribution'.

Mean Median Mode Range

In math world everything must be exact, this could be explained in different ways of calculating the center of a set of data. They are:

Mean

Mean can be explained as the addition of all the values in the set and divided by the no. of values. Mean can be denoted by μ for the given overall population and the mean of the same can be denoted by x̄ (for arithmetic mean).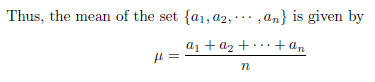

Mean Formula

Mean is delicate to any modification in values, different than mode and median, where a modification to an utmost value normally does not have any effect.

Disadvantages of Mean

Mean has one of the disadvantage that is a smallest numeral of utmost values could deform its value. For instance, the mean of the set {1, 1, 1, 4, 4, 8, 8, 8, 280} is 35, although most of them are very small members. A variation known as the trimmed mean, here the least and greatest quarters of the values are abstracted prior to the mean is accepted, could resolve this problem.

Median

Median can be explained as the middle number of a set of numerals ordered in numeric order. Whenever the amount of set values are even, and so the median is defined as the sum of the two centre values that is divided by 2.

Median is not impacted by the extreme value's magnitude (lowest or greatest). Hence, it's helpful as it's not impacted by one or two abnormally least or biggest values and since it's really simple to compute. (E.g., to find a relatively precise average lifespan of a specific type of incandescent lamp, you could quantify the median life by setting up numerous incandescent lamps and valuating how much time was taken before half of them died out. Choices would likely involve quantifying the lifespan of each incandescent lamp.

Mode

Mode is the most regular value in any set. A set may have much more than one mode and if it has two then it's stated as bimodal.

Example: Mode of {2, 4, 4, 6, 7, 9} is 4.
Modes of {2, 3, 4, 6, 7, 7, 12, 16, 16, 18} are 7 and 16. Hence, this set is bimodal.

Range

Range can be explained as the difference between the greatest and the lowest values of the set.

Calculating range of any set is quiet simple also its not very helpful as it depends on the extreme values that might be distorted. Another form similar to trimmed mean is inter-quartile range or IQR that is the range of set with lowest and greatest quarters eliminated. For example, medians Q1 and Q3 are the lowest and greatest halves of data set, hence the IQR is written as Q3 - Q1.