Definite Integrals

Fundamental Theorem of Calculus: It states that the sum of small changes in any quantity over a period of time adds up to the total quantity.

In the below figure I have shown the function F(x) and I need to find the area of the above curve I take the bounded values of the curve a and b start summing up taking the small values of dx considering a small rectangle and extending the same area throughout the curve.

This is taken as the integral for the whole area under the curve between the limits a and b.

So fundamental theorem takes the form

$\int_{a}^{b}(F(x)dx$ = F(b) - F(a) to find the area under a curve.

F(x) is the integral of f(x);

F(b) is the value of the integral at the upper limit, x=b; and

F(a) is the value of the integral at the lower limit, x=a.

This expression is called a definite integral.

$Definite Integrals$

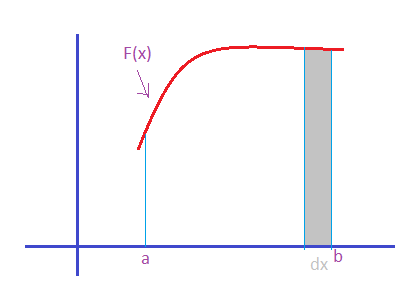
So it clearly says the area can be found out using the above integral and is also known as definite integral.

Applications of Definite Integrals

Its usage can be seen in a vast number of applications such as finding the volume of solids of revolution, area enclosed between two curves and integral as sum of limit.

Properties of Definite Integrals

Consider 2 functions f(x) and g(x) which are continues functions then

$\int_{a}^{b} (f(x)+g(x))=\int_{a}^{b}f(x) + \int_{a}^{b} g(x)$

$\int_{a}^{a}f(x)=0$

$\int_{a}^{b}f(x) = \int_{a}^{d}f(x)+\int_{d}^{b}f(x)$

$\int_{b}^{a}f(x)= -\int_{a}^{b}f(x)$

For arbitrary numbers a and b and d belongs to [a, b].

Definite Integrals Solved Problems

Example 1: Find the integral and then write the upper and lower limits with square brackets, as follows:

$\int_{2}^{3}(5x^{4})+2x+6$

[x 5 + $x^2$ + 6x] 2, 3

The upper and lower limits are written like this to mean they will be substituted into the expression in brackets.

Next, substitute 5 (the upper limit) into the integral:

[(2-3)⁵ + (2-3) 2 + 6(2-3)]= -1 +1+ 6(-1) = -6

Example 2: Find the integral $\int_{1}^{2}(5+7x^{6})$

Solution : $\int_{1}^{2}(5+7x^{6})$

5x + x⁷

$5(2-1) + (2-1)^7$

5 + 1 = 6

Example 3: Find the work done if a force F(x) = 5x - 3 N is acting on an object and moves it from x = 1 to x = 6.

Solution: $\int_{1}^{6}(5x-3)$

[$5x^2 - 3x$]

$5(6-1)^2 - 3(6-2)$

125 - 12

113 joules.

Example 4: The expression, v, for velocity in terms of t, the time, we can find the displacement S of a moving object from time t = 0 to time t = 6 by integration is given by $\int_{0}^{6}(v dt)$

If V is given by t².

Then [$\frac{t^3}{3}$] (After integrating)

216/18 unit/sec.

Next Chapters

Number Theory	Linear Equation	Set Theory	Math Fractions
Math Functions	Pyramid	Calculus	Cone
Cylinder	Chain Rule	Limits and Continuity	Prime Factorization
Square Roots and Cube Roots	Parabola	Distance Formula	Definite Integrals
Interest	Simple Interest	Compound Interest	Area of Irregular Figures